Busca em Strings com Algoritmo Z

May 11, 2025

Continuando a abordagem que trouxemos no post anterior, onde tratamos algumas operações básicas de strings, iremos falar sobre o Algoritmo Z, que é uma boa ferramenta para resolvar problemas de busca em strings. O Algoritmo Z é um algoritmo eficiente para encontrar todas as ocorrências de um padrão em uma string, e é especialmente útil quando o padrão é pequeno em comparação com a string de texto.

O Algoritmo Z

Por definição, temos que no desenvolvimento do algoritmo, criamos um vetor Z, onde Z[i] representa o comprimento do maior prefixo da substring que começa em i e é também sufixo da string. O algoritmo Z é construído em tempo linear, O(n), onde n é o tamanho da string. O algoritmo Z é útil para resolver problemas de busca de padrões, como encontrar todas as ocorrências de um padrão em uma string. A ideia básica é construir o vetor Z e, em seguida, usar esse vetor para encontrar as ocorrências do padrão na string. Dada uma string ( s ) de tamanho ( n ), o algoritmo Z calcula um array ( Z ) onde cada elemento ( Z[i] ) representa o comprimento da maior substring que começa na posição ( i ) e que é também um prefixo da string ( s ).

Por exemplo, para a string:

s = "aabcaabxaaaz" -> Z = [0, 1, 0, 0, 3, 1, 0, 0, 2, 2, 1, 0] s = "aaaaa" -> Z = [0, 4, 3, 2, 1]

Nesse exemplo abaixo, fiz um gif para acompanhar o funcionamento do algoritmo Z.

s = "abcabcabc" -> Z = [0, 0, 0, 6, 0, 0, 3, 0, 0]

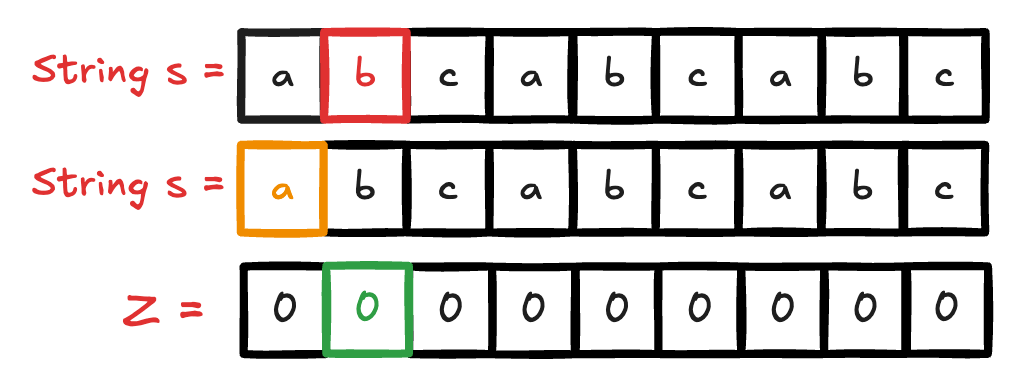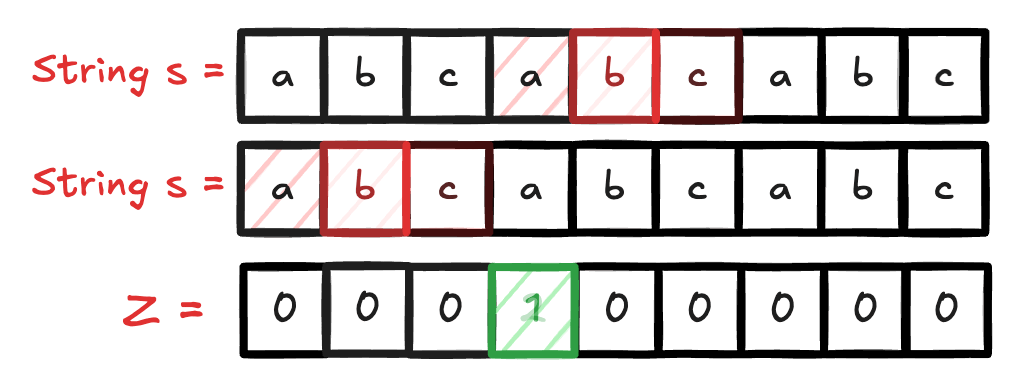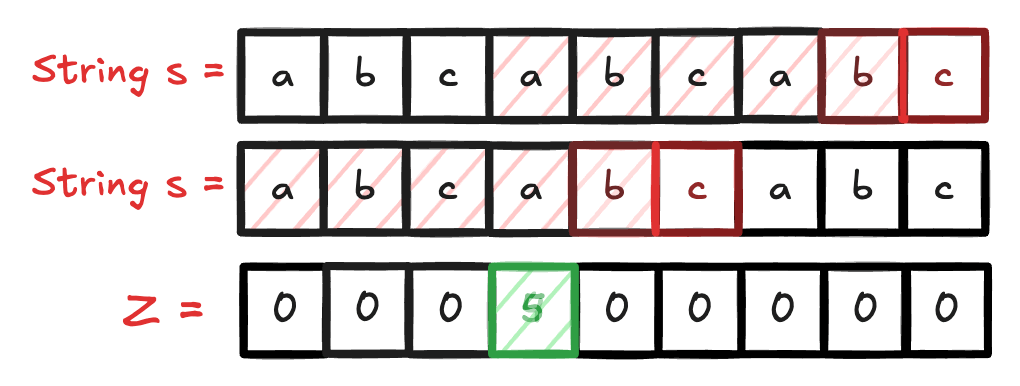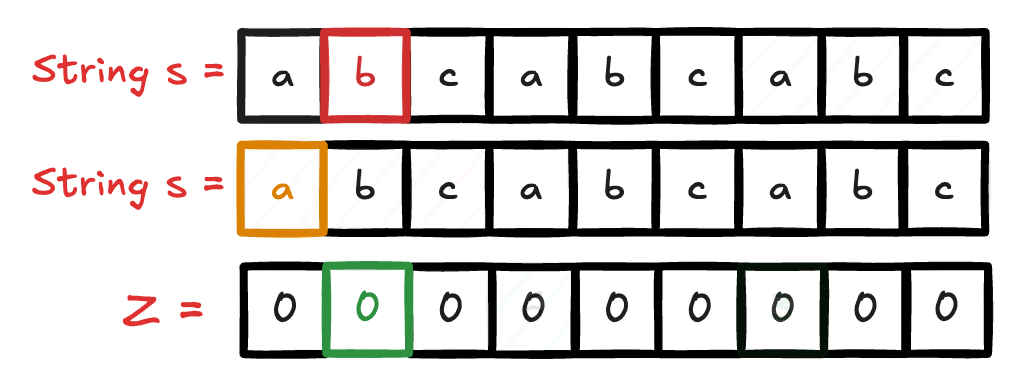
My helpful Gif

Como o Algoritmo Z funciona?

A ideia por trás do algoritmo é evitar comparações redundantes. Quando encontramos um prefixo que coincide com um sufixo, podemos usar essa informação para pular algumas comparações. Garantindo que cada caractere da string seja processado no máximo uma vez, resultando em complexidade ( O(n) ).

Passos principais

Inicialize o vetor Z com zeros. Cria-se o array ( Z ) com zeros e define-se uma janela ([l, r]) que indica a faixa da substring que coincide com o prefixo da string.
Iteração pela string: Para cada posição ( i ) de 1 até ( n-1 ): Se ( i > r ), não há janela válida que ajude, então compara-se diretamente o prefixo com a substring começando em ( i ), atualizando ( Z[i] ), ( l ) e ( r ). Se ( i < r ), aproveita-se o valor de ( Z[i-l] ) para definir um valor inicial para ( Z[i] ). Se necessário, expande-se a comparação além de ( r ).
Atualização do vetor Z: Sempre que uma nova correspondência maior é encontrada, atualiza-se a janela ([l, r]).
Implementação:

// Source: https://cp-algorithms.com/string/z-function.html
vector<int> z_function(string s) {
    int n = s.size();
    vector<int> z(n);
    int l = 0, r = 0;
    for(int i = 1; i < n; i++) {
        if(i < r) {
            z[i] = min(r - i, z[i - l]);
        }
        while(i + z[i] < n && s[z[i]] == s[i + z[i]]) {
            z[i]++;
        }
        if(i + z[i] > r) {
            l = i;
            r = i + z[i];
        }
    }
    return z;
}

Corretude do Algoritmo Z

Um ponto importante que acho interessante nesse algoritmo, é a forma como ele lida com as redundâncias. Quando fui tentar codar o algoritmo, por conta própria, apenas me guiando pela lógica, ficou incorreto quando chegava em certos casos, um deles era o seguinte:

string s = "aaaaaaa"

Meu Z estava incorreto justamente por não tratar corretamente a janela ([l,r]).

Mas relendo o artigo que temos no cp-algorithms, consegui entender que faz sentido! (meio obvio, mas é um passo importante). Então, recomendo que tente replicar a lógica de Z, pois é simples, é um bom exercicio para enxergar um pouco mais do que eu vivenciei. Ou nao!

Continuando, vamos abordar sobre a corretude, que por sinal é muito bem escrita no artigo do cp-algorithms.

Z funciona, pois:

A janela ([l, r]) sempre representa a maior substring que coincide com o prefixo e que termina na posição ( r ).
Para cada índice ( i ), se ( i ) está fora da janela, fazemos comparações diretas para calcular ( Z[i] ).
Se ( i ) está dentro da janela, podemos usar o valor já calculado em ( Z[i-l] ) para evitar comparações redundantes, pois essa informação representa uma correspondência já conhecida dentro da janela.
Quando o valor de ( Z[i-l] ) ultrapassa o limite da janela, o algoritmo expande a janela para a direita, comparando os caracteres além de ( r ).
Essa estratégia garante que cada caractere seja comparado no máximo uma vez, o que assegura a complexidade linear ( O(n) ).

Aplicações do Algoritmo Z

1. Busca de Substring

Uma aplicação que aparece mais frequentemente trata-se de dado um texto t e um padrão p, o problema é encontrar todas as ocorrências de p dentro de t.

Para resolver esse problema com o algoritmo Z, construímos uma nova string s = p + ‘#’ + t, onde ‘#’ é um caractere separador que não ocorre nem em p nem em t. (É importante que o caractere separador não pertença a p ou t, para evitar erros na construção do vetor Z).

Calculamos o array Z para o novo s. Para cada posição i no intervalo [0; comprimento(t) - 1], consideramos o valor k = Z[i + comprimento(p) + 1]. Se k for igual a comprimento(p), então há uma ocorrência do padrão p na posição i do texto t.

Essa abordagem tem complexidade O(comprimento(t) + comprimento(p)), sendo muito eficiente mesmo para textos e padrões grandes.

2. Número de Substrings Distintas

Uma aplicação bem interessante do algoritmo Z é contar o número de substrings distintas em uma string. Dada uma string s de comprimento n, queremos contar o número de substrings distintas presentes em s.

Uma forma de resolver isso é iterativamente, adicionando um caractere c ao final de s e recalculando o número de substrings distintas. Para isso, consideramos a string invertida t = (s + c) invertida. Calculamos a função Z de t e encontramos o seu valor máximo z_max.

O número de novas substrings que aparecem ao adicionar c é igual a comprimento(t) - z_max, pois os prefixos de t que aparecem em outras posições não são novas substrings.

Essa solução tem complexidade O(n²) para uma string de comprimento n, mas pode ser otimizada para O(n) em casos específicos.

// usamos o Z descrito anteriormente.
int main() {
    string s; cin >> s;
    int totalDistinct = 0;
    string current = "";
    for(int i = 0; i < s.size(); i++){
        current += s[i];
        string t = current;

        reverse(t.begin(), t.end());

        auto z = z_function(t);
        int zmax = 0;
        for(int val : z){
            zmax = max(val,zmax);
        }
        totalDistinct += ((int)t.size() - zmax);
    }

    cout << totalDistinct << endl;
    return 0;
}

Note que:

Construímos a string current adicionando um caractere por vez.
Invertendo current e calculando o array Z, encontramos o maior prefixo que ocorre também no meio da string invertida.
A quantidade de novas substrings adicionadas é o tamanho da string menos esse valor máximo de Z.
Somamos esse valor ao total de substrings distintas.

3. Compressão de Strings (encontrar menor substring que se repete)

Dada uma string ( s ) de comprimento ( n ), queremos encontrar sua representação “compactada” mais curta: uma string ( t ) de menor comprimento tal que ( s ) seja a concatenação de uma ou mais cópias de ( t ).

Para isso, calculamos a função Z de ( s ) e verificamos todos os índices ( i ) que dividem ( n ). Para o menor ( i ) que satisfaça ( i + Z[i] = n ), a string ( s ) pode ser representada como múltiplas cópias da substring ( s[0..i-1] _.

    string s; cin >> s;
    auto z = z_function(s);

    int compressLength = n; // por padrão a resposta é a string nao comprimida

    for(int i = 1; i < n; i++){
        if(n % i == 0 && i + z[i] == n){
            compressLength = i;
            break;
        }
    }

    cout << compressLength << endl;

Conclusão

Z é uma boa ferramenta, e por ser simples de codar e entender, consegue ser implementado mais intuitivamente. No entanto, existem situações em que precisamos lidar com problemas mais complexos, como buscar múltiplos padrões simultaneamente, ou otimizar ainda mais a eficiência da busca em casos específicos. Para esses desafios e para lidar com outros tipos de problemas utilizamos algoritmos como KMP (Knuth-Morris-Pratt) e Aho-Corasick oferecem soluções especializadas e eficientes.