Joao Canuto Blog

Introdução a Algoritmos em Strings em C++

Algoritmos

Definição :

Um algoritmo é uma sequência finita de passos bem definidos para resolver um problema ou realizar uma tarefa. Na ciência da computação, algoritmos são essenciais para manipular dados, realizar cálculos, buscar informações e muito mais.

A estrutura típica de um algoritmo envolve:

Complexidade de um Algoritmo

A complexidade de um algoritmo é um conceito que usamos para medir o uso de recursos principalmente tempo (tempo de execução) e espaço (memória), em função do tamanho da entrada. Na maior parte dos problemas de programação competitiva, exploramos principalmente o tempo de execução quando desenvolvemos alguma solução. Nesse contexto, nos problemas é dado um tempo máximo que seu código ( algoritmo ) deve entregar uma solução no pior dos casos do problema.

Definição :

Quando importa saber da complexidade ?

Dado o problema:

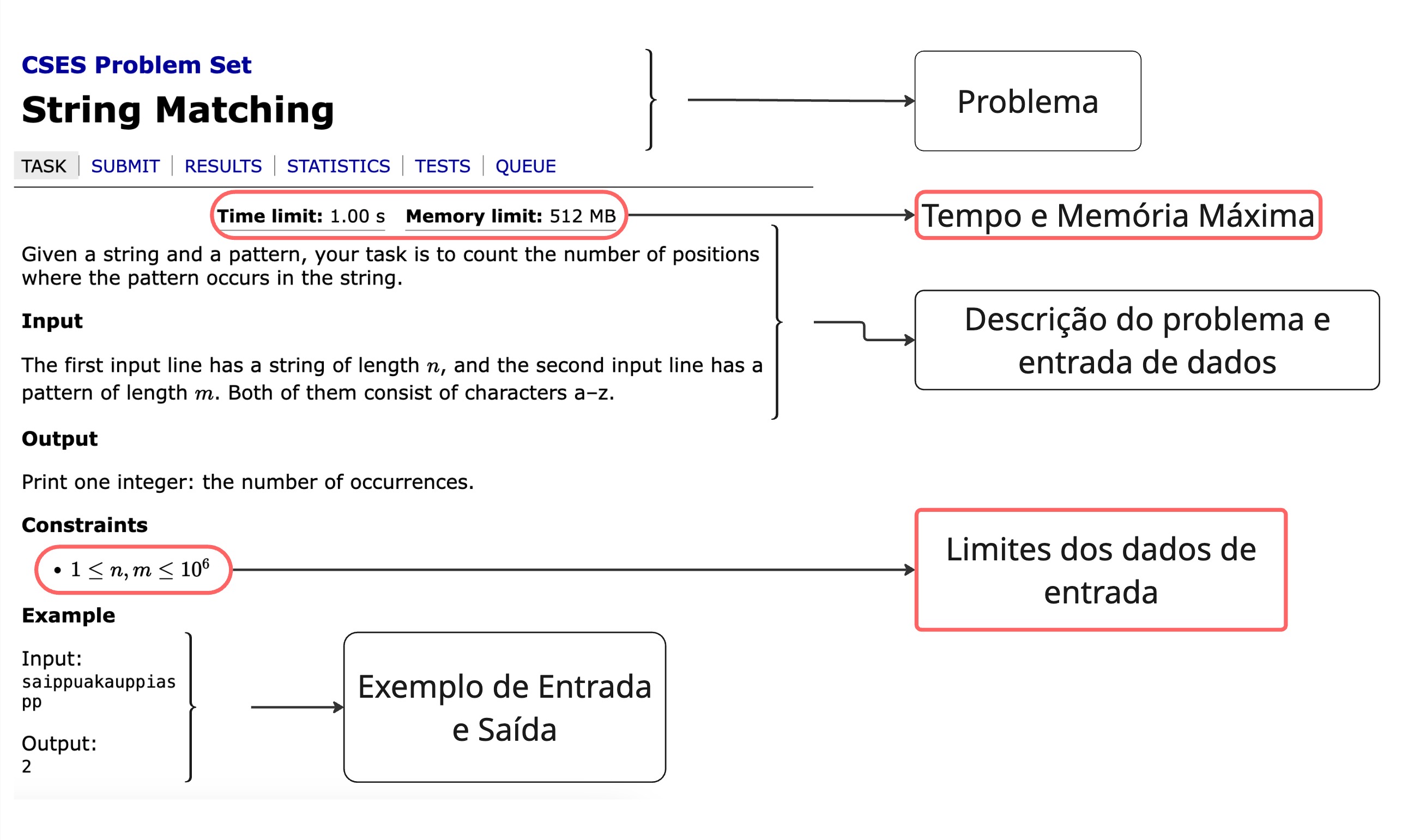
My helpful screenshot

Marquei e descrevi a estrutura comum de um problema que encontramos em competições. E deixei diferenciado de vermelho os campos que são relevantes no contexto de complexidade:

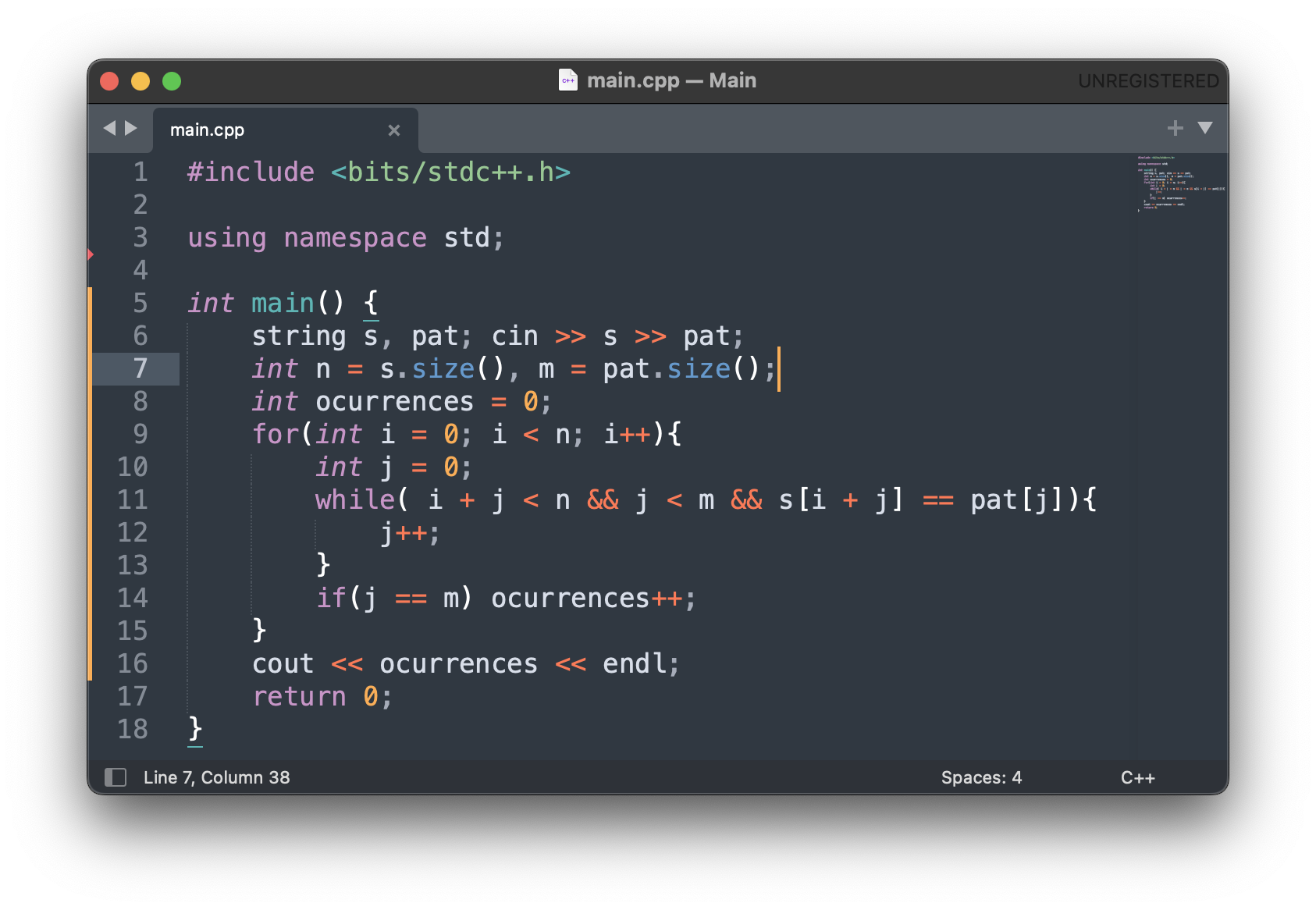
My helpful screenshot 2

E de resultado:

My helpful screenshot 2

Pronto, testamos no primeiro caso, e aparentemente funciona. De certa forma, mas vamos submeter o problema para que ele teste em todos os casos teste do problema:

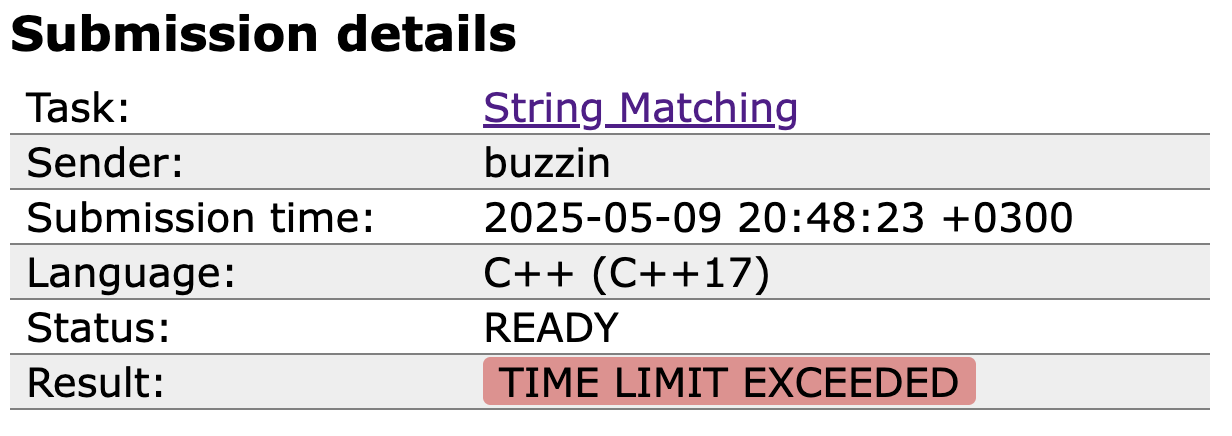
My helpful screenshot 2

Famoso TLE!! Aqui vai um disclaimer sobre um ponto importante sobre o que esse tempo significa. Você pode tentar comparar a execução do código na sua máquina, mas vai ser bem diferente do tempo obtido quando seu código é avaliado pelo judge. Isso acontece pq seu código roda em um ambiente muito mais limitado que o que você tem disponível.

Dessa forma, quando nos referirmos a Tempo de Execução, temos mais ou menos uma noção de tempo para seu código executar, digamos N operações.

Precisamos melhorar a complexidade

Enxergamos nesse caso que nosso algoritmo não atendeu ao tempo limite da questão, então precisamos adaptar o código. Esse caso de otimização conseguimos encontrar alguns casos de uso, exemplo:

Solução :

Utilizar estruturas e algoritmos eficientes para encontrar substrings repetidas rapidamente, como o array Z. Em todos esses casos, a melhoria da complexidade do algoritmo é importante para garantir que o código execute dentro dos limites de tempo, especialmente quando lidamos com grandes volumes de dados. Adaptar o código para usar algoritmos eficientes não é apenas uma questão de performance, mas muitas vezes uma necessidade para viabilizar a solução do problema.

Resolvendo nosso problema de Tempo:

Vamos adaptar nosso código para um algoritmo mais eficiente , utilizaremos o Z-Algorithm:


#include <bits/stdc++.h>
using namespace std;

// Função para calcular o array Z
vector<int> calcularZ(const string &s) {
    int n = (int)s.size();
    vector<int> Z(n, 0);
    int l = 0, r = 0;
    for (int i = 1; i < n; i++) {
        if (i > r) {
            l = r = i;
            while (r < n && s[r - l] == s[r]) r++;
            Z[i] = r - l;
            r--;
        } else {
            int k = i - l;
            if (Z[k] < r - i + 1) {
                Z[i] = Z[k];
            } else {
                l = i;
                while (r < n && s[r - l] == s[r]) r++;
                Z[i] = r - l;
                r--;
            }
        }
    }
    return Z;
}

int main() {
    ios::sync_with_stdio(false);
    cin.tie(nullptr);

    string s, pat;
    cin >> s >> pat;

    string concat = pat + "#" + s;  // '#' é um caractere que não aparece em s nem pat
    vector<int> Z = calcularZ(concat);

    int m = (int)pat.size();
    int ocurrences = 0;
    for (int i = m + 1; i < (int)concat.size(); i++) {
        if (Z[i] == m) {
            ocurrences++;
        }
    }

    cout << ocurrences << "\n";
    return 0;
}

Z é um algoritmo bem interessante e bem inicial quando falamos de busca por padrão em textos. E para nosso problema será bem suficiente. Irei abordar esse algoritmo no artigo seguinte a esse, que iremos explorar as informação que conseguimos quando implementamos Z. De maneira resumida, Z retorna um array onde cada posição indica o comprimento da maior substring que começa naquela posição e que coincide com o prefixo da string. Então para checarmos se um padrão acontece no texto, basta encontrar os caso em que Z[i] == m, m sendo o tamanho do nosso padrão. E como resultado, quando submetemos nossa solução, temos:

My helpful screenshot 2

Z, possui complexidade de O(n + m), ou seja, dizemos que tem complexidade linear. E por curiosidade, no CSES, na página da submissão encontramos os tempos referentes a cada teste, e o teste. Dessa forma conseguimos identificar o pior caso, que foi:

My helpful screenshot 2 My helpful screenshot 2

Coloquei o input em um contador de carateres e temos n = 1.000.000 e m = 1.000.000, o limite máximo exposto no problema.

Strings em C++:

Finalizando complexidade, vamos cobrir a base de Strings que irá ser útil para servir de base para explorararmos nos próximos artigos e enxergarmos como algumas operações básicas, fornecidades na biblioteca padrão de strings em C++, tem complexidade alta.

O que é uma string?

Em C++, uma string é uma sequência de caracteres que representa texto. A biblioteca padrão oferece a classe std::string, que facilita a manipulação de textos de forma segura e eficiente.

Desde o C++11, e aprimorada até o C++23, a classe std::string é amplamente utilizada por sua facilidade de uso e integração com outras partes da linguagem.

Operações comuns em strings

Algumas das operações mais comuns com strings em C++23 incluem:

Conclusão

Entender a estrutura dos algoritmos e sua complexidade é fundamental para desenvolver soluções eficientes. No contexto de strings em C++, a classe string oferece uma interface poderosa para manipulação de texto, mas é importante conhecer a complexidade das operações para otimizar o desempenho.

Com essa base, podemos explorar algoritmos avançados de processamento de strings, como o algoritmo Z, KMP e Aho-Corasick.